Dot Product
(requires JavaScript)
-
Which of the following expression are meaningful? Which are meaningless? Explain.b, c, and d are meaningful.
-
Find the dot product of two vectors if their lengths are and and the angle between them is .
-
Find if , .
-
Find if and .
-
If is a unit vector, find and .
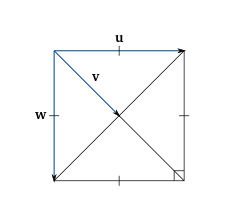
From the figure, , and . The angle between and is , and the angle between and is . So we can write
and
-
Find the angle between vectors and .
-
Determine whether given vectors are orthogonal, parallel, or neither.
- , .
- , .
- , .
- , .
Neither, orthogonal, orthogonal, parallel. -
Find two unit vectors that make an angle of with .
-
Find the scalar and vector projections of onto , where and .
,
.
-
Suppose that and are non-zero vectors. Under what circumstances is
-
An intelligent robot exerts a horizontal force of lb on a crate as it pushes it up a ramp that is feet long and inclined at an angle of above the horizontal. Find the work done on the box.ft-lb.
-
Find the angle between a diagonal of a cube and one of its edges.