Double Integrals Over General Regions

(requires JavaScript)

1. Evaluate the iterated integral ${\displaystyle {\int }_0^1{\int }_0^{x^2}\left(x+2y\right)dydx}$.
   ${\displaystyle \frac{9}{20}}$
2. Evaluate the double integral ${\displaystyle \underset{D}{\iint }x\cos <!--FUNCTION\; APPLICATION-->\left(y\right)dA}$ if $D$ is bounded by $y=0$, $y=x^2$, and $x=1$.
   ${\displaystyle \frac{1-\cos <!--FUNCTION\; APPLICATION-->\left(1\right)}{2}}$
3. Evaluate the double integral ${\displaystyle \underset{D}{\iint }{y}^{3}dA}$ if $D$ is a triangle with vertices $\left(0,2\right)$, $\left(1,1\right)$, and $\left(3,2\right)$.
   ${\displaystyle \frac{147}{20}}$
4. Find the volume of the solid under the plane $x+2y-z=0$ and above the region bounded by $y=x$ and $y=x^4$.
   ${\displaystyle \frac{7}{18}}$
5. Find the volume of the solid bounded by the planes $x=0$, $y=0$, $z=0$, and $x+y+z=1$.
   ${\displaystyle \frac{1}{6}}$
6. Find the volume of the solid bounded by the cylinder $x^2+y^2=1$ and the planes $y=z$, $x=0$, and $z=0$ in the first octant.
   ${\displaystyle \frac{1}{3}}$

7. Sketch the region of integration and change the order of integration for

   ${\displaystyle {\int }_1^2{\int }_0^{\ln <!--FUNCTION\; APPLICATION-->\left(x\right)}f<!--FUNCTION\; APPLICATION-->\left(x,y\right)dydx}$.

   ${\displaystyle {\int }_0^{\ln <!--FUNCTION\; APPLICATION-->\left(2\right)}{\int }_{e^y}^{2}f<!--FUNCTION\; APPLICATION-->\left(x,y\right)dxdy}$.

8. Evaluate the integral

   ${\displaystyle {\int }_0^3{\int }_{y^2}^{9}y\cos <!--FUNCTION\; APPLICATION-->\left(x^2\right)dxdy}$

   by reversing the order of integration.

   ${\displaystyle \frac{1}{4}\sin <!--FUNCTION\; APPLICATION-->\left(81\right)}$

9. Express $D$ as a union of Type 1 and/or Type 2 regions and evaluate the integral ${\displaystyle \underset{D}{\iint }{x}^{2}dA}$. The curve plotted in the figure is $y=1-x^2$.

   

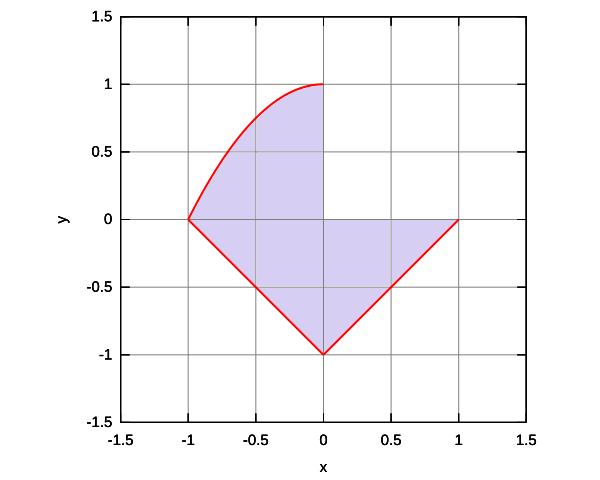
10. The double integral over a region $D$ can be written as a sum of iterated integrals

    ${\displaystyle \underset{D}{\iint }f<!--FUNCTION\; APPLICATION-->\left(x,y\right)dA={\int }_0^1{\int }_0^{2y}f<!--FUNCTION\; APPLICATION-->\left(x,y\right)dxdy+{\int }_1^3{\int }_0^{3-y}f<!--FUNCTION\; APPLICATION-->\left(x,y\right)dxdy}$.

    Sketch the region $D$ and express the double integral as an iterated integral with reversed order of integration.