Double Integrals In Polar Coordinates
(requires JavaScript)
-
For each region shown, decide whether to use polar or rectangular coordinates and write the iterated integral , where is an arbitrary continuous function.
a.
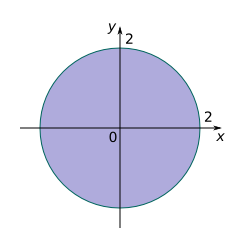 b.
b. 
c.
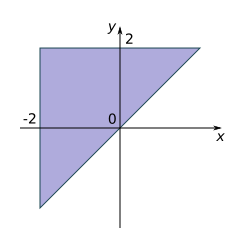 d.
d. 
e.
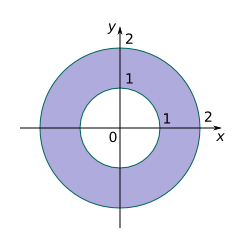 f.
f. 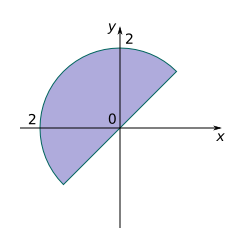
-
Sketch the region whose area is given by the integral and evaluate the integral
-
Evaluate the integral
by changing to polar coordinates. Here is the region that lies above the within the circle .
-
Evaluate the integral
by changing to polar coordinates, given that
-
Use polar coordinates to find the volume of the solid above the cone and below the sphere .
-
Use polar coordinates to find the volume of the solid inside both the cylinder and the ellipsoid .
-
Evaluate the iterated integral by converting to polar coordinates.
-
Evaluate the iterated integral by converting to polar coordinates.