Line Integrals

(requires JavaScript)

1. Evaluate the line integral ${\displaystyle {\int }_{C}yds}$, where $C$ is the curve $x=t^2$, $y=t$, $0\le t\le 2$.
   ${\displaystyle \frac{17\sqrt{17}-1}{12}}$
2. Evaluate the line integral ${\displaystyle {\int }_{C}x{y}^{4}ds}$, where $C$ is the right half of the circle $x^2+y^2=16$.
   $1638.4$
3. Evaluate the line integral ${\displaystyle {\int }_{C}x{y}^{3}ds}$, where $C$ is the curve $x=4\sin <!--FUNCTION\; APPLICATION-->\left(t\right)$, $y=4\cos <!--FUNCTION\; APPLICATION-->\left(t\right)$, $z=3t$, $0\le t\le \pi /2$.
   $320$
4. Evaluate the line integral ${\displaystyle {\int }_{C}x{e}^{yz}ds}$, where $C$ is the line segment from $\left(0,0,0\right)$ to $\left(1,2,3\right)$.
   ${\displaystyle \frac{\sqrt{14}\left(e^6-1\right)}{12}}$
5. Evaluate the line integral ${\displaystyle {\int }_{C}xydx+\left(x-y\right)dy}$ where $C$ consists of line segments from $\left(0,0\right)$ to $\left(2,0\right)$ and from $\left(2,0\right)$ to $\left(3,2\right)$.
   ${\displaystyle \frac{17}{3}}$
6. Evaluate the line integral ${\displaystyle {\int }_C\sin <!--FUNCTION\; APPLICATION-->\left(x\right)dx+\cos <!--FUNCTION\; APPLICATION-->\left(y\right)dy}$ where $C$ consists of the top half of the unit circle from $\left(1,0\right)$ to $\left(-1,0\right)$ and the line segment from $\left(-1,0\right)$ to $\left(-2,3\right)$.
7. Evaluate the line integral ${\displaystyle {\int }_C{x}^{2}dx+y^{2}dy+z^{2}dz}$, where $C$ consists of line segments from $\left(0,0,0\right)$ to $\left(1,2,-1\right)$, and from $\left(1,2,-1\right)$ to $\left(3,2,0\right)$.
8. Evaluate the line integral ${\displaystyle {\int }_C\mathbf{F}•d\mathbf{r}}$ where $\mathbf{F}<!--FUNCTION\; APPLICATION-->\left(x,y\right)=x^2{y}^3\mathbf{i}-y\sqrt{x}\mathbf{j}$ and $C$ is given by the vector function $\mathbf{r}<!--FUNCTION\; APPLICATION-->\left(t\right)=t^2\mathbf{i}-t^3\mathbf{j}$, $0\le t\le 1$.
   ${\displaystyle -\frac{59}{105}}$
9. Evaluate the line integral ${\displaystyle {\int }_C\mathbf{F}•d\mathbf{r}}$ where $\mathbf{F}<!--FUNCTION\; APPLICATION-->\left(x,y,z\right)=⟨z,y,-x⟩$ and $C$ is given by the vector function $\mathbf{r}<!--FUNCTION\; APPLICATION-->\left(t\right)=⟨t,\sin <!--FUNCTION\; APPLICATION-->\left(t\right),\cos <!--FUNCTION\; APPLICATION-->\left(t\right)⟩$, $0\le t\le \pi$.
10. A thin wire is bent into the shape of a semicircle $x^2+y^2=4$, $x\ge 0$. If the linear density is a constant $k$, find the mass and the centroid of the wire.
    $2\pi k$ and $\left(4/\pi ,0\right)$
11. Find the work done by the force field $\mathbf{F}<!--FUNCTION\; APPLICATION-->\left(x,y,z\right)=⟨y+z,x+z,x+y⟩$ on a particle that moves along the line segment from $\left(1,0,0\right)$ to $\left(3,4,2\right)$.
    $26$
12. 1. An intelligent robot ($160$ kg) is carrying a canister with oil ($25$ kg) up a helical ramp that encircles a rocket with a radius $20$ m. If the rocket is $90$ m high and the robot makes exactly $3$ complete revolutions, how much work is done by the robot against gravity while climbing to the top?
    2. If there is a hole in the canister and $9$ kg of oil leaks out at a steady rate during the ascent, how much work is done?

13. An object moves along the curve $C$ shown in the figure from $\left(1,2\right)$ to $\left(9,8\right)$. The lengths of the vectors in the force field $\mathbf{F}$ are measured in newtons by the scales on the axes. Estimate the work done by $\mathbf{F}$ on the object.

    

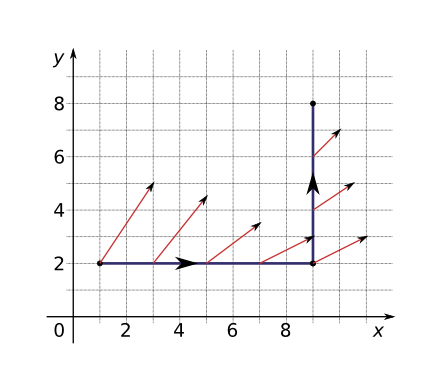    $22$ J