Parametric Surfaces

(requires JavaScript)

1. Identify the surface with the vector equation

   $\mathbf{r}<!--FUNCTION\; APPLICATION-->\left(u,v\right)=2\sin <!--FUNCTION\; APPLICATION-->\left(u\right)\mathbf{i}+3\cos <!--FUNCTION\; APPLICATION-->\left(u\right)\mathbf{j}+v\mathbf{k}$

   where $0\le v\le 2$.

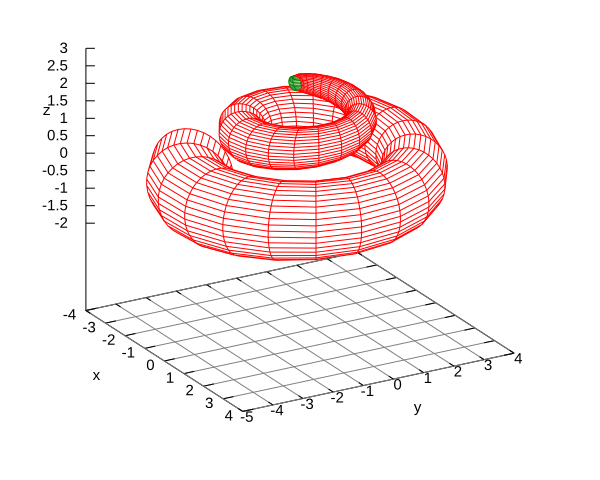
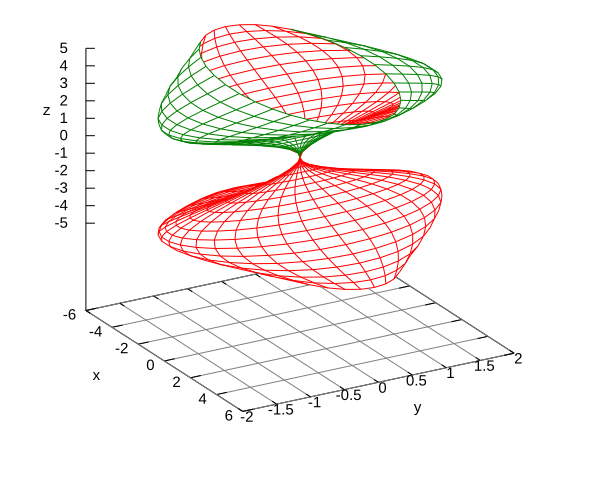
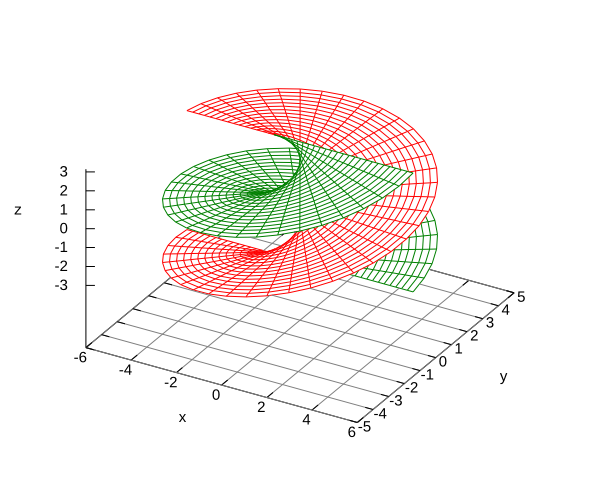
2. Match the equations with the graphs, explain.

   1. $\mathbf{r}<!--FUNCTION\; APPLICATION-->\left(u,v\right)=⟨\cos <!--FUNCTION\; APPLICATION-->\left(v\right),\sin <!--FUNCTION\; APPLICATION-->\left(v\right),u⟩$
   2. $\mathbf{r}<!--FUNCTION\; APPLICATION-->\left(u,v\right)=⟨u\cos <!--FUNCTION\; APPLICATION-->\left(v\right),u\sin <!--FUNCTION\; APPLICATION-->\left(v\right),u⟩$
   3. $\mathbf{r}<!--FUNCTION\; APPLICATION-->\left(u,v\right)=⟨u\cos <!--FUNCTION\; APPLICATION-->\left(v\right),u\sin <!--FUNCTION\; APPLICATION-->\left(v\right),v⟩$
   4. $x=u^3,y=u\sin <!--FUNCTION\; APPLICATION-->\left(v\right),z=u\cos <!--FUNCTION\; APPLICATION-->\left(v\right)$
   5. $x=\left(u-\sin <!--FUNCTION\; APPLICATION-->\left(u\right)\right)\cos <!--FUNCTION\; APPLICATION-->\left(v\right)$,
      $y=\left(1-\cos <!--FUNCTION\; APPLICATION-->\left(u\right)\right)\sin <!--FUNCTION\; APPLICATION-->\left(v\right)$,
      $z=u$.
   6. $x=\left(1-u\right)\left(3+\cos <!--FUNCTION\; APPLICATION-->\left(v\right)\right)\cos <!--FUNCTION\; APPLICATION-->\left(4\pi u\right)$,
      $y=\left(1-u\right)\left(3+\cos <!--FUNCTION\; APPLICATION-->\left(v\right)\right)\sin <!--FUNCTION\; APPLICATION-->\left(4\pi u\right)$,
      $z=3u+\left(1-u\right)\sin <!--FUNCTION\; APPLICATION-->\left(v\right)$.

   1. 
   2. 
   3. 
   4. 
   5. 
   6. 
3. Find parametric equations for the surface obtained by rotating the curve $y=e^{-x}$, $0\le x\le 3$, about the $x\text{-axis}$ and use them to graph the surface.
   $x=x,y=e^{-x}\cos <!--FUNCTION\; APPLICATION-->\left(\theta \right),z=e^{-x}\sin <!--FUNCTION\; APPLICATION-->\left(\theta \right),0\le x\le 3$

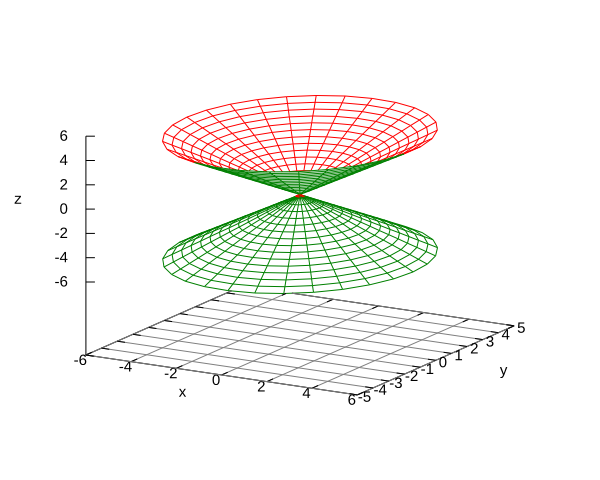
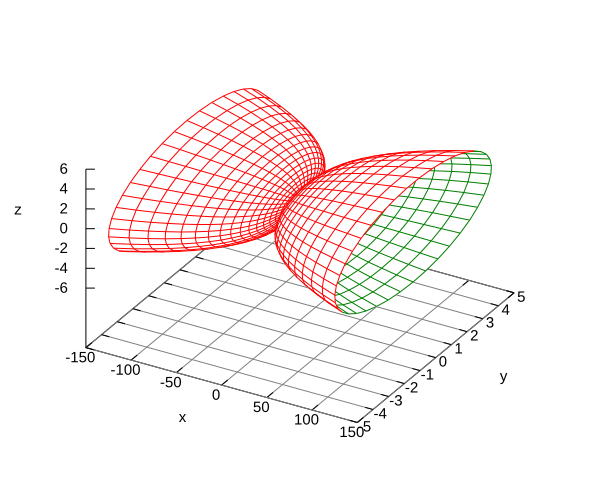
4. Match the shown surfaces with their parametrizations. Justify your choices.

   ${\mathbf{r}}_1<!--FUNCTION\; APPLICATION-->\left(u,v\right)=⟨\sin <!--FUNCTION\; APPLICATION-->\left(u\right)\cos <!--FUNCTION\; APPLICATION-->\left(v\right),\sin <!--FUNCTION\; APPLICATION-->\left(u\right)\sin <!--FUNCTION\; APPLICATION-->\left(v\right),\cos <!--FUNCTION\; APPLICATION-->\left(u\right)⟩$

   ${\mathbf{r}}_2<!--FUNCTION\; APPLICATION-->\left(u,v\right)=⟨u,v,u^2-v^2⟩$

   ${\mathbf{r}}_3<!--FUNCTION\; APPLICATION-->\left(u,v\right)=⟨u\cos <!--FUNCTION\; APPLICATION-->\left(v\right),u,u\sin <!--FUNCTION\; APPLICATION-->\left(v\right)⟩$

   ${\mathbf{r}}_4<!--FUNCTION\; APPLICATION-->\left(u,v\right)=⟨u,e^u\cos <!--FUNCTION\; APPLICATION-->\left(v\right),e^u\sin <!--FUNCTION\; APPLICATION-->\left(v\right)⟩$

   ${\mathbf{r}}_5<!--FUNCTION\; APPLICATION-->\left(u,v\right)=⟨u,\sqrt{1+u^2}\cos <!--FUNCTION\; APPLICATION-->\left(v\right),\sqrt{1+u^2}\sin <!--FUNCTION\; APPLICATION-->\left(v\right)⟩$

   ${\mathbf{r}}_6<!--FUNCTION\; APPLICATION-->\left(u,v\right)=⟨u,v,u^3+v^3⟩$

   
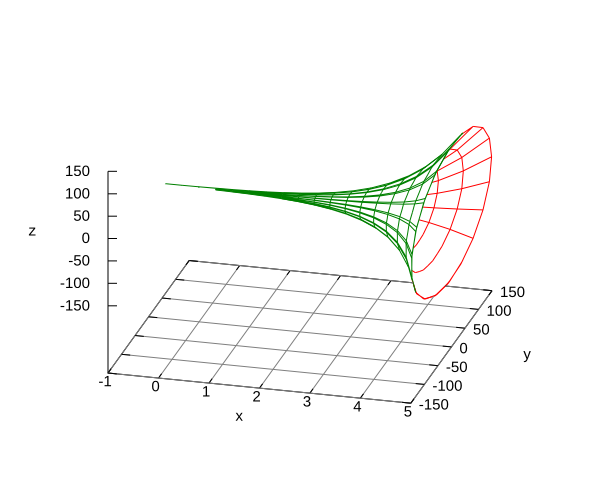
   Surface 1.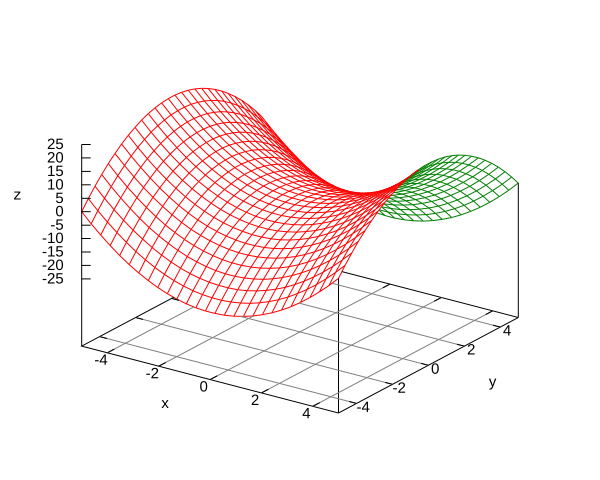

   
   Surface 2.

   ${\mathbf{r}}_4$ and ${\mathbf{r}}_2$.