Vector Functions And Space Curves

(requires JavaScript)

1. Find the domain of the vector function $\mathbf{r}<!--FUNCTION\; APPLICATION-->\left(t\right)=⟨t^2,\sqrt{t-1},\sqrt{5-t}⟩$.
   $\left[1,5\right]$
2. Find ${\displaystyle \underset{t\to 0^{}}{\lim }<!--FUNCTION\; APPLICATION-->⟨\arctan <!--FUNCTION\; APPLICATION-->\left(t\right),e^{-2t},\frac{\ln <!--FUNCTION\; APPLICATION-->\left(t\right)}{t}⟩}$
   The limit does not exist because ${\displaystyle \frac{\ln <!--FUNCTION\; APPLICATION-->\left(t\right)}{t}}$ diverges to infinity as $t$ tends to $0$ from above.
3. Sketch the curve given by equation $\mathbf{r}<!--FUNCTION\; APPLICATION-->\left(t\right)=⟨\sin <!--FUNCTION\; APPLICATION-->\left(t\right),t⟩$ and indicate the direction in which $t$ increases.
4. Sketch the curve given by equation $\mathbf{r}<!--FUNCTION\; APPLICATION-->\left(t\right)=⟨1,\cos <!--FUNCTION\; APPLICATION-->\left(t\right),2\sin <!--FUNCTION\; APPLICATION-->\left(t\right)⟩$ and indicate the direction in which $t$ increases.
5. Sketch the curve given by equation $\mathbf{r}<!--FUNCTION\; APPLICATION-->\left(t\right)=t^2\mathbf{i}+t\mathbf{j}+2\mathbf{k}$ and indicate the direction in which $t$ increases.
6. Find a vector equation and parametric equations for the line segment joining $P\left(1,0,1\right)$ and $Q\left(2,3,1\right)$.
   Vector equation: $\mathbf{r}<!--FUNCTION\; APPLICATION-->\left(t\right)=⟨2,3,1⟩-⟨1,3,0⟩t$.
   Parametric equations: $x=2-t$, $y=3-3t$, $z=1$, where $0\le t\le 1$.
7. Match parametric equations with the given graphs. Explain.

   1. $x=\cos <!--FUNCTION\; APPLICATION-->\left(4t\right),y=t,z=\sin <!--FUNCTION\; APPLICATION-->\left(4t\right)$.
   2. $x=t,y=t^2,z=e^{-t}$.
   3. $x=t,y=\frac{1}{1+t^2},z=t^2$.
   4. $x=e^{-t}\cos <!--FUNCTION\; APPLICATION-->\left(10t\right),y=e^{-t}\sin <!--FUNCTION\; APPLICATION-->\left(10t\right),z=e^{-t}$.
   5. $x=\cos <!--FUNCTION\; APPLICATION-->\left(t\right),y=\sin <!--FUNCTION\; APPLICATION-->\left(t\right),z=\sin <!--FUNCTION\; APPLICATION-->\left(5t\right)$.
   6. $x=\cos <!--FUNCTION\; APPLICATION-->\left(t\right),y=\sin <!--FUNCTION\; APPLICATION-->\left(t\right),z=\ln <!--FUNCTION\; APPLICATION-->\left(t\right)$.

   I. II.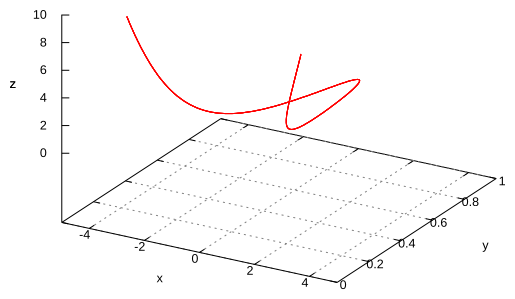

   III. 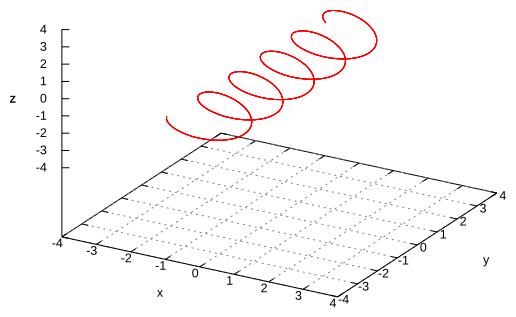IV.

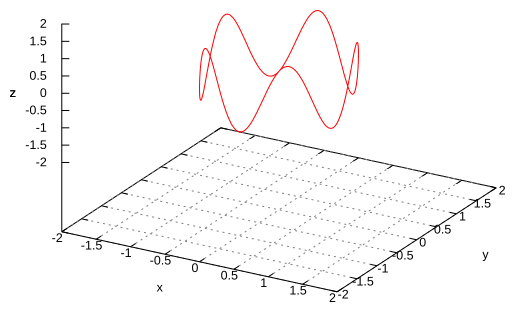
   V. 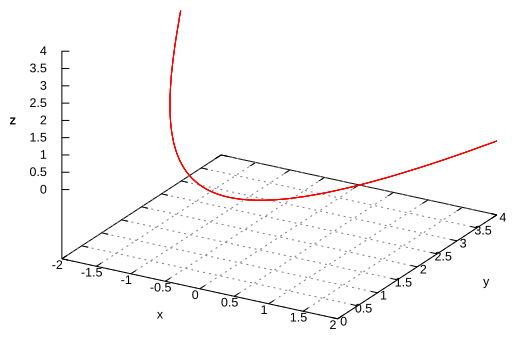VI.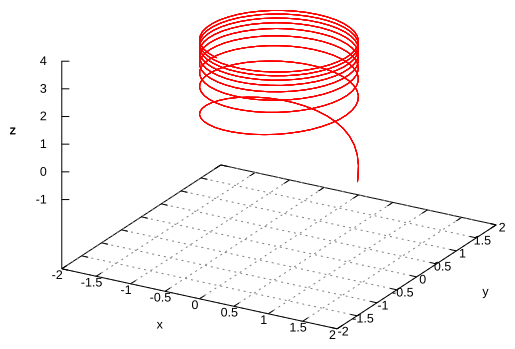

   III, V, II, I, IV, VI.
8. Use a computer to graph the curve given by the equation $\mathbf{r}<!--FUNCTION\; APPLICATION-->\left(t\right)=⟨\sin <!--FUNCTION\; APPLICATION-->\left(t\right),\sin <!--FUNCTION\; APPLICATION-->\left(2t\right),\sin <!--FUNCTION\; APPLICATION-->\left(3t\right)⟩$.
9. Two neutrons travel along the space curves ${\mathbf{r}}_1<!--FUNCTION\; APPLICATION-->\left(t\right)=⟨t,t^2,t^3⟩$ and ${\mathbf{r}}_2<!--FUNCTION\; APPLICATION-->\left(t\right)=⟨1+2t,1+6t,1+14t⟩$. Will they collide? Do their paths intersect?
   No collision; intersections at $⟨1,1,1⟩$ and $⟨2,4,8⟩$.