Vectors
(requires JavaScript)
-
Write each combination of directed line segments as a single directed line segment.

-
Given and , find a vector with representation given by the directed line segment . Draw and the equivalent representation starting at the origin.
-
Find the sum of vectors and and illustrate geometrically.
-
Find , , , and , where and .
-
Find a unit vector with the same direction as .
-
The two forces and with magnitudes lb and lb respectively, act on an object at a point as shown in the figure. Find the resultant force acting at as well as its magnitude and its direction. (Indicate the direction by finding the angle shown in the figure.)
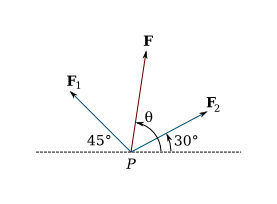 ,
,
lb,
. -
Velocities have both direction and magnitude and thus are represented by vectors. The magnitude of a velocity is called speed. Suppose that a wind is blowing from the direction NW at a speed of km/h. (This means that the direction from which the wind blows is west of northerly direction.) A pilot is steering a helicopter in the direction NE at an airspeed (speed in still air) of km/h. The true course, or track, of an aircraft is the direction of the resultant of the velocity vectors of the aircraft and the wind. The ground speed of the aircraft is the magnitude of the resultant. Find the true course and the ground speed of the helicopter.
-
Chains and m in length are fastened to a suspended decoration. The decoration has a mass of kg. The chains, fastened at different heights, make angles of and with the horizontal. Find the tension in each chain and the magnitude of each tension.
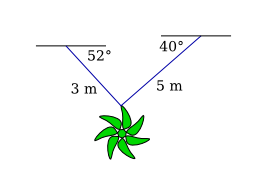
-
The tension at each end of the rope has magnitude N. What is the weight of the rope?

Let and be the tensions. By symmetry, their horizontal components cancel and their vertical components are equal. The magnitudes of vertical components of and add up to . Since the chain is at rest, the force must have the same magnitude as that of the force due to gravity, , where . So we can write
, and hence
,
[kg]. -
Use vectors to prove that the line joining the midpoints of two sides of a triangle is parallel to the third side and half its length.